Functions y k x and its schedule. Linear function. Task at home

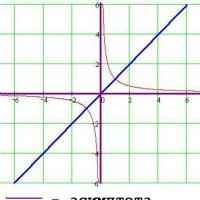
Consider the function y \u003d k / y. The graph of this feature is a line called in math hyperbole. General view of hyperboles, presented in the figure below. (The graph shows the function y equal to K divided by x, in which K is equal to one.)

It can be seen that the schedule consists of two parts. These parts refer to the branches of hyperboles. It is also worth noting that each branch of hyperboles is suitable in one of the directions and closer and closer to the coordinate axes. The axis of the coordinates in this case is called asymptotes.

In general, any straight lines to which the chart of the function is infinitely approaching, but does not reach them, are called asymptotes. Hyperbolas, like a parabola, there are axis of symmetry. For hyperboles shown in the figure above, it is straight y \u003d x.

Now we'll figure it out with two general cases of hyperball. The graph of the function y \u003d k / x, for k ≠ 0, will be hyperbole, the branches of which are located either in the first and third coordinate corners, at k\u003e 0, or in the second and fourth coordinate angles, when<0.

The main properties of the function y \u003d k / x, when k\u003e 0

Function graph Y \u003d k / x, when k\u003e 0

5. Y\u003e 0 for x\u003e 0; y6. The function decreases both on the interval (-∞; 0) and in the interval (0; + ∞).

10. Area of \u200b\u200bfunction values \u200b\u200bTwo open gaps (-∞; 0) and (0; + ∞).

The main properties of the function y \u003d k / x, when k<0

Function graph Y \u003d k / x, when k<0

1. Point (0; 0) Center of symmetry hyperboles.

2. The axes of the coordinates - asymptotes of hyperboles.

4. The field of determining the function of all x, except x \u003d 0.

5. Y\u003e 0 at x0.

6. The function increases both on the interval (-∞; 0) and on the interval (0; + ∞).

7. The function is not limited to the bottom, none.

8. The function has no greatest nor the least values.

9. The function is continuous on the interval (-∞; 0) and on the interval (0; + ∞). It has a gap at point x \u003d 0.

Linear function called the type of type y \u003d kx + bdefined on the set of all valid numbers. Here k. - angular coefficient (valid), b. – free member (valid), x. - Independent variable.

In a particular case, if k \u003d 0., we get a constant function y \u003d B.whose graph is direct, parallel OX axis passing through a point with coordinates (0; b).

If a b \u003d 0.then we get a function y \u003d kx., which is direct proportionality.

b. – length Cutwhich cuts back on the Oy axis, counting from the start of coordinates.

Geometric meaning of the coefficient k. – tilt angle Direct to the positive direction of the OX axis is counted counterclockwise.

Properties of linear function:

1) The area of \u200b\u200bdefinition of the linear function is the entire real axis;

2) If a k ≠ 0The region of the values \u200b\u200bof the linear function is the entire real axis. If a k \u003d 0.The region of the values \u200b\u200bof the linear function consists of b.;

3) The parity and oddness of linear function depend on the values \u200b\u200bof the coefficients k. and b..

a) b ≠ 0, k \u003d 0, Consequently, y \u003d b - even;

b) b \u003d 0, k ≠ 0, Consequently y \u003d kx is odd;

c) b ≠ 0, k ≠ 0, Consequently y \u003d kx + b - common function;

d) b \u003d 0, k \u003d 0, Consequently y \u003d 0 - both even and odd function.

4) The property of the frequency is the linear function does not possess;

5) Point of intersection with axes of coordinates:

OX: y \u003d kx + b \u003d 0, x \u003d -b / k, Consequently (-b / k; 0) - Point of intersection with the axis of the abscissa.

Oy: y \u003d 0k + b \u003d b, Consequently (0; b) - Point of intersection with ordinate axis.

Note. If b \u003d 0. and k \u003d 0., then function y \u003d 0. Drawn to zero with any value of the variable h.. If a b ≠ 0 and k \u003d 0., then function y \u003d B. does not turn to zero under any values \u200b\u200bof the variable h..

6) The intervals of the alignment depend on the coefficient K.

a) k\u003e 0; KX + B\u003e 0, KX\u003e -B, X\u003e -B / K.

y \u003d kx + b - positive as x. of (-b / k; + ∞),

y \u003d kx + b - negative for x. of (-∞; -b / k).

b) k.< 0; kx + b < 0, kx < -b, x < -b/k.

y \u003d kx + b - positive as x. of (-∞; -b / k),

y \u003d kx + b - negative for x. of (-b / k; + ∞).

c) k \u003d 0, b\u003e 0; y \u003d kx + b positive throughout the definition area

k \u003d 0, b< 0; y = kx + b Negative on the entire definition area.

7) Linear function monotonic intervals depend on the coefficient k..

k\u003e 0., Consequently y \u003d kx + b increases throughout the field of definition,

k.< 0 , Consequently y \u003d kx + b decreases throughout the field of definition.

8) The linear function graph is straight. To build a direct enough to know two points. The right position on the coordinate plane depends on the values \u200b\u200bof the coefficients k. and b.. Below is a table that illustrates it clearly.

In this video, you will get acquainted with the function \u003d k / x, k - the coefficient that can take different values, except 0. Let's consider the case when k \u003d 1 \u003d\u003e y \u003d 1 / x. To build a graph of this function, we will recall the material that was in the previous video, namely: We will select several arbitrary values \u200b\u200bfor x and substitute them in formula \u003d k / x.

This will give us the opportunity to calculate the values \u200b\u200bof the dependent variable y. Selection of values \u200b\u200band calculations Y will be built in two stages: first give the argument positive values, and then negative.

Using the formula y \u003d k / x, we find the value of Y. If x \u003d 1, then y \u003d 1. We will select several arguments on their own.

In the case when x \u003d 3, then y \u003d 1/3; x \u003d 5, then y \u003d 1/5; x \u003d 7, then y \u003d 1/7.

And when x \u003d 1/3, then y \u003d 3; x \u003d 1/5, then y \u003d 5; x \u003d 1/7, then y \u003d 7.

Make a table:

In the case when x \u003d 1, then \u003d -1, x \u003d -3, then y \u003d -1/3; x \u003d -5, then y \u003d -1/5; x \u003d -7, then \u003d -1/7.

And when x \u003d -1/3, then y \u003d -3; x \u003d -1/5, then y \u003d 5; x \u003d -1/7, then y \u003d -7.

Make a table:

We construct the data of the point on the coordinate Plane of the How and connect them.

An example with other coordinates and a sequence of building a schedule can be seen in the video.

Also in the video tutorial you will familiarize yourself with the main geometric properties of hyperboles.

The hyperbole, like Parabola, has symmetry. If you spend directly through the origin of the coordinate 0, it will cross the hyperbola at two points, which lie on the line on opposite sides of the point 0 and on equal distance from it. Thus, 0 will be the center of symmetry hyperboles, and it will be symmetrical about the origin.
Symmetric, relative to the start of the coordinates, part of the hyperboles are called its branches.
One branch of the hyperbole is located near the abscissa axis, the other is near the ordinate. In such cases, the corresponding straight lines are called asymptotes. This means that the hyperbole has two asymptotes - the axis x and the axis y.
In addition to the center of symmetry, the hyperbole has the axis of symmetry.

The graph of the function y \u003d k / x, as K is not equal to 0 is a hyperbole whose branches are in 1 and 3 coordinate planes, in the case when K\u003e 0, and 2 and 4 k\u003e 0, and 2 and 4 coordinate planes when K.< 0. (0,0) - точка центра симметрии гиперболы, а осями координат являются её асимптоты. Функцию y = k/x называют обратно пропорциональной, в силу того, что её величины - x и у, являются обратно пропорциональными, а число k - это коэффициент обратной пропорциональности.